Making movie recommendations

July 17, 2016

I did my summer internship at Microsoft Technology Center, Bangalore. There, I worked on the problem of recommending movies. This post talks about how the solution that I developed works.

A screenshot of the final app displaying movies similar to Cinderella

The Problem Statement

Given a set of user ratings for a given set of movies, predict the rating of a user for a movie.

The problem has three cases:

Existing user, existing movie
New user, existing movie
Existing user, new movie

Types of Recommender Systems

By the type of data, Recommender Systems can be classified into two types depending on the type of data that they use. They are :

Explicit : votes, ratings and reviews.
Implicit : the user isn’t asked whether they like an item or not. Instead, their behaviour is observed. This includes clicks, items added to cart, items bought etc.

I worked on Explicit Movie Rating Data from GroupLens. The solution has been tested on the same.

The Dataset

The GroupLens MovieLens 100k dataset consists of 1682 movies rated by 943 users. Each user has rated at least 20 movies, a total of 10,000 ratings. Ratings are positive integers from 1 to 5.

Sno.	UserId	MovieId	Rating	Timestamp
0	196	242	3	881250949
1	186	302	3	891717742
2	22	377	1	878887116
3	244	51	2	880606923
4	166	346	1	886397596

⊕
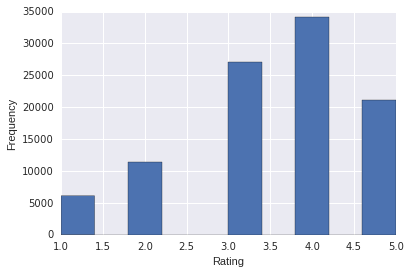
The frequency distribution of the movie ratings data

The evaluation metric

The accuracy of the predictions was measured by the Root Mean Squared Error(RMSE).

$RMSE = \sqrt{ \frac{ \sum_{i=1}^{n} predicted_i - actual_i }{n} }$

The solution

Preprocessing

The ratings table was converted into a movie by user matrix of dimension (1682, 943). Since, not every user rated every movie, there were a lot of missing values. They were designated by a 0.

$\left [ \begin{array}{ccccccc} 5 & 0 & 0 & 0 & \dots & 3\\ 0 & 2 & 0 & 3 & \dots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \\ 0 & 0 & 4 & 0 & \dots &1\\ \end{array} \right ]$

As a result, more than 97 % of the matrix consists of zeros. So, to efficiently store the matrix, a sparse representation was used.

Predicting Movie Ratings

Now, given the matrix representation, by computing distance based scores, we can find :

Similar Users
Similar Movies

Similarity is related to distance by :

$similarity \propto \frac{1}{distance}$

Similar Users

If we can find users similar to the current one, we can recommend movies that the similar users liked and have not been watched by the current user.

Also, a reasonable way of predicting the current user’s rating is by taking an average of the ratings of k - similar users weighted by their similarity to current user.

$r_{um} = \frac{ \sum_{i=1}^{k} r_{im} \cdot s_{iu} } { \sum_{i=1}^{k} s_{iu} }$

where,

$r_{ij}$ is the rating of movie $j$ by user $i$ .
$s_{ij}$ is the similarity between users $i$ and $j$ .

This method has the following shortcomings :

The number of users is much larger than the number of movies in a real-life dataset. Thus, the number of computations of user-user similarity becomes infeasible.
Since the average user does not rate a lot of movies, the most similar users might still have a much different taste in movies.
User preferences are continuously changing. Thus a 10 year old rating might not still be relevant.

Similar Movies

To overcome the shortcomings of user-user similarity based predictions, movie-movie similarity is used.

Here, the same similarity metric is used to compute similar movies. These similar movies can be shown along with the description of the movie.

To make a rating prediction, we can take an average of k - similar movies that have been rated by the current user weighted by their similarity to the current movie.

$r_{um} = \frac{ \sum_{i=1}^{k} r_{ui} \cdot s_{mi} } { \sum_{i=1}^{k} s_{mi} }$

where,

$r_{ij}$ is the rating of movie $j$ by user $i$ .
$s_{ij}$ is the similarity between movies $i$ and $j$ .

This approach is better as :

The number of movies is generally less than the total number of users. Hence, the computations are less.
While user preferences evolve over time, the movie similarity derived from their ratings, result in a stable movie to movie similarity score. Hence, the movie similarities for existing movies can be pre-computed and saved.

Choosing a similarity metric

Following distance metrics are widely used and were considered :

Euclidean Distance
Manhattan Distance
Cosine Distance

Euclidean Distance

The most common way of finding distance between two data points.

In two dimensions, distance between $a(a_1, a_2)$ and $b(b_1, b_2)$ ,

$euclidean \space distance = \sqrt{ (a_1 - b_1)^{2} + (a_2 - b_2)^{2} }$

Generally, in n-dimensions, distance between $a(a_1, \dots, a_n)$ and $b(b_1, \dots, b_n)$ ,

$euclidean \space distance = \sqrt{ \sum_{i=1}^{n} (a_i - b_i)^{2} }$

This however does not work well in our case. This is because there are a large number of missing ratings which are represented by a zero. The euclidean distance interprets the zero as a rating that is lower than 1.

Manhattan Distance

This is another common way of finding distance.

In two dimensions, distance between $a(a_1, a_2)$ and $b(b_1, b_2)$ ,

$manhattan \space distance = \sqrt{ |a_1 - b_1| + |a_2 - b_2| }$

Generally, in n-dimensions, distance between $a(a_1, \dots, a_n)$ and $b(b_1, \dots, b_n)$ ,

$manhattan \space distance = \sqrt{ \sum_{i=1}^{n} |a_i - b_i| }$

Manhattan distance fails too, due to the same reason.

Cosine Distance

This metric basically finds the cosine of the angle between the lines joining the data points to the origin.

In two dimensions, distance between $a(a_1, a_2)$ and $b(b_1, b_2)$ ,

$cosine \space distance = \frac{ (a_1 \cdot b_1) + (a_2 \cdot b_2) } { \sqrt{ (a_1^2 + a_2^2) } \cdot \sqrt{ (b_1^2 + b_2^2) } }$

Generally, in n-dimensions, distance between $a(a_1, \dots, a_n)$ and $b(b_1, \dots, b_n)$ ,

$cosine \space distance = \frac{ \sum_{i=1}^{n} (a_i \cdot b_i)} { \sqrt{ (\sum_{i=1}^{n} a_i^2) } \cdot \sqrt{ (\sum_{i=1}^{n} b_i^2) } }$

This cosine distance takes a different approach to the problem and relies on multiplication instead of addition or subtraction. Thus, if either of the movies have not been rated by a given user that set of data points is discarded due to incompleteness.

Cosine similarity can be defined as,

$cosine\_similarity(a, b) = 1 - cosine\_distance(a, b)$

Conclusion

In the implementation, I used the cosine similarity metric to find movies similar to a given movie to improve discovery of movies. The metric was implented in python and deployed on Azure ML as a web service.

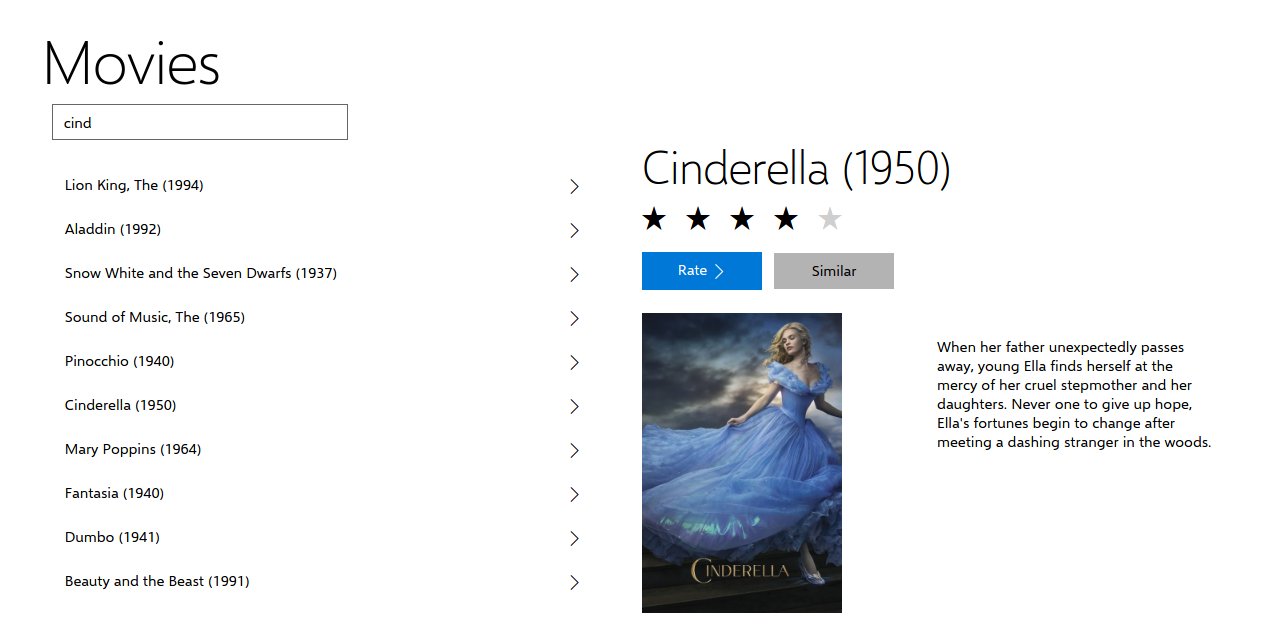
For the movie Cinderella, the movie simililarity service predicts

The Lion King
Aladdin
Snow White and the seven dwarfs
Sound of music

as similar movies. This seems to works pretty well - even better than a genre match for surfacing movies.

The ratings predicted by this method gives an RMSE of 1.05 which, however, is not good enough.